みなさま、こんにちは。当記事では素朴な疑問「割り算において、0で割れないのは何故?」について私なりの考えを投稿します。
はじめに
一昔前、小学生の算数の宿題に「18÷0=?」という問題が出題されていたことがXを起点に様々なSNSで反響がありましたね。今でも検索すれば出てきます。
皆さんの答えは如何でしょう。
- 掛け算同様、0で割ると商(答え)は0になる
- 割り算において、0で割ることはできない
恐らくはこの2択になると思います。そして多くの人は後者を選択されるかと思います。はい、正解は後者の「0除算はできない」となります。プログラミングのjavaでも演算において0除算が発生すると「ArithmeticException」がスローされ処理が中断します。
でも、何故0除算が禁じられているのか皆さんは説明できますか?私も完璧には説明できないですが、私なりの個人的な考えを次の見出しで説明します。
0除算が禁じられている理由(個人的な考え)
これから算数の問題を以下に6問並べます。
- ①1÷0.1=?
- ②1÷0.01=?
- ③1÷0.001=?
- ④1÷(-0.1)=?
- ⑤1÷(-0.01)=?
- ⑥1÷(-0.001)=?
さて、皆さんはこれらの問題に答えられますか?勿論答えられますよね。特に答えが重要ではないので、ぱっぱと答えを書きます。
- ①10
- ②100
- ③1000
- ④-10
- ⑤-100
- ⑥-1000
これらの答えを見て何か気がつきませんか?
「①〜③」については、①から徐々に0に近づけています。「0.1より0.01の方が0に近い」「0.01より0.001の方が0に近い」です。そして、0に近づけば近づくほど商(答え)は大きくなっていきます。
「④〜⑥」については、④から徐々に0に近づけています。「-0.1より-0.01の方が0に近い」「-0.01より-0.001の方が0に近い」です。そして、0に近づけば近づくほど商(答え)は小さくなっていきます。
これらの結果をグラフにするとこんな感じになります。
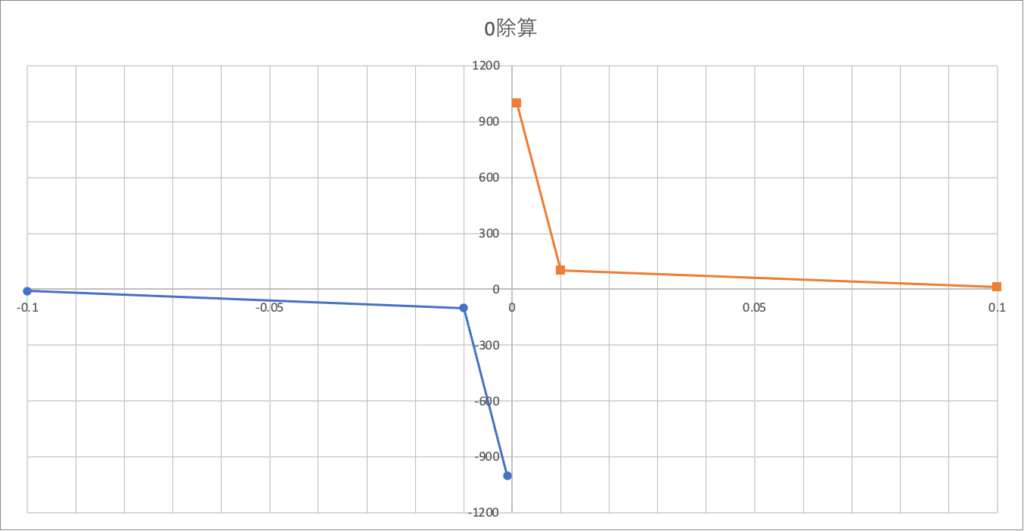
青線:0より小さい 橙線:0より大きい
何が言いたいかというと、
- 0より小さい数字から0に近づけていくと、商(答え)は小さくなり続ける
- 0より大きい数字から0に近づけていくと、商(答え)は大きくなり続ける
となりますね。
この法則を参考に
1÷0
を求めようとすると、恐らく商(答え)は「解なし」になるのでは無いかと考えています。(要は0になった時、めちゃくちゃ大きい数字になるかめちゃくちゃ小さい数字になるか定まらないからです。)
以上のことから、一つの値に絞ることが出来なくなるため0除算は禁じられているものと私は考えます。
0除算を許容するとどうなる?(個人的な考え)
まぁ、結論を先に書くと「数字、数学が全て破綻する」です。これには2種類の考え方があります。まずは1つ前の見出しで取り扱った「1÷0」について考えてみましょう。
小学生の頃、割り算を習う学年でこのような考え方を習ったと思います。
「x ÷ y = z」 → 「x = y × z」
例:「8÷4=2」 → 「8=4×2」
この考え方で「1÷0」を解こうと思うと
「1=0×□」となります。
そして、□に当てはまる数字こそが「1÷0」の商となるのですが、掛け算の規則で「0には何を掛けても0である」ということから、□に当てはまる数字なんてありませんよね?
したがって、「解なし」が答えとなります。(前の見出し通りですね)
これだけだと、何の問題もなさそうですよね。数学の方程式に関する問題でも「解なし」が答えになることもあるので、問題ないように思えます。
では、続いて「0÷0」について考えてみましょう。問題なのはこれです。
上記のように、掛け算で商を求めようとすると
「0=0×□」となります。
そして、□に当てはまる数字こそが「0÷0」の商となるのですが、掛け算の規則で「0には何を掛けても0である」ということから、□には何の数字を入れても成り立ちそうですよね?
と言うことは、、、
「0=0×1」が成り立ち、
「0=0×2」も成り立つ。
したがって、「1=2」である。と言うことになってしまいます。これが成り立ってしまうと、生活の身近にある「お金」にも影響してきます。要は、「10億円持っている超富裕層」も「貯金10万円の人」も同じってことになります。
だってそうですよね?1億円で売られているスーパーカーも1円あれば買えてしまえる訳ですし、10億円だって1円と価値は同じってことになりますからね。勿論、お金以外の数字を取り扱う分野全てがぐちゃぐちゃになります。(道路や鉄道の制限速度や、ファイルサイズ、通信速度など)
以上のことから、冒頭に書いた通り「数字、数学が全て破綻する」という結論に至ると考えています。
さいごに
ここまで私なりの0除算ができない理由についてご紹介しましたがいかがでしょうか。ご不明点や誤りなどありましたら、ご指摘のほどお願いいたします。
そして、最後にちょっとした豆情報をご紹介。iPhone(iOS18)での話ですが、電卓機能において「0を0で除算する」時と「0以外を0で除算する」時でエラーメッセージが異なります。ご存じでしたか?
0を0で除算

0以外を0で除算

- 「0を0で除算」した場合は「判定不能」と表示されます。
- 「0以外を0で除算」した場合は「ゼロで割っています」と表示されます。
もしかすると、「解なし」と「どの数字でも答えになり得る」の2種類を表現しているんですかね?